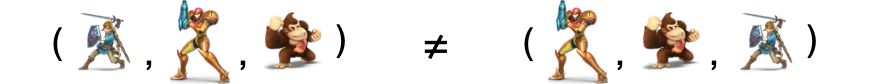Sets
CSE 16: Applied Discrete Mathematics
Instructor: Owen Arden
Winter 2023
Sets? Seriously?
Sets, Venn diagrams, union, intersection… isn’t this like
elementary school stuff?
Here we are going to formalize the treatment of
sets
Sets play a foundational role in math (and memes):
- Russell was dedicated to the idea that mathematics was just logic +
set theory
Introduction to sets
- Sets are a basic building block of mathematics
- Set theory gives a language to describe all types of mathematical
structures
- Created by Georg Cantor (1845-1918)
- Set theory is itself an important branch of mathematics
- Many different systems of axioms have been used to formalize
theories of sets
- Here we will use “naive set theory.”
![]()
Georg
Cantor (before 19th century mental health care)
![]()
Georg Cantor (after 19th century mental health
care)
Definitions: sets and
elements
- Set
-
A set is an unordered collection of objects.
The “naive” treatment of sets is easy to
understand, but leads to some paradoxes. It is enough to prove the
theorems we care about here, though.
Objects in a set are called elements or
members of the set, and we say that a set contains its
elements.
- We write \(a \in
A\) to denote that \(a\) is an
element of set \(A\).
- If \(a\) is not a
member of \(A\), we write \(a \not\in A\)
In general, sets are often written using
uppercase letters and their elements using lowercase letters.
Universal set and empty set
- The universal set \(U\) is
the set containing everything currently under consideration.
- May be implicit or explicit
- Contents depend on the context
- One of the things later theorists got rid of to avoid
paradoxes.
- The empty or “null” set is the set with no elements. Usually written
\(\emptyset\), but also \(\{\}\)
Example: the smash universe
Representing sets: roster
method
- The roster method lists the members of a set
- Ellipses can be used if the pattern is clear
- \(S = \{a, b, c, d, ..., z\}\)
- Ellipses can also be for infinite patterns
Roster method examples
- Set of all vowels in English alphabet
- \(V = \{a, e, i, o,
u\}\)
- Set of all odd positive integers less than 10:
- Set of all positive integers less than 100:
- \(S = \{1,2,3,...,
99\}\)
- Set of all integers less than 0:
- \(S = \{...,
-3,-2,-1\}\)
Representing sets: set
builder notation
- Example: Positive rational numbers
\[\mathbb{Q}^{+} = \{ x \in \mathbb{R} : x
= \frac{p}{q} \text{ for some positive integers } p,q \text{ where } q
\neq 0 \}\]
Some important sets
- Natural numbers
- \(\mathbb{N} = \{ 0, 1, 2, 3, 4, …
\}\)
- Integers
- \(\mathbb{Z} = \{ …,-4,-3,-2,-1,0, 1, 2,
3, 4, … \}\)
- Positive integers
- \(\mathbb{Z}^{+} =
\{1,2,3,4,…\}\)
- Rational numbers
- \(\mathbb{Q} = \{p/q : p \in \mathbb{Z}, q
\in \mathbb{Z}^{+}\}\)
- Real numbers
- \(\mathbb{R} = \{ \text{any decimal number
of arbitrary precision} \}\)
- Irrational numbers
- \(\{ x: x \in \mathbb{R} \text{ and } x
\not\in \mathbb{Q} \}\)
Representing sets: interval
notation
- Interval notation describes a set in terms of an
interval boundary.
\([a,b] = \{x | a \leq x \leq b
\}\)
\([a,b) = \{x | a \leq x \lt b
\}\)
\((a,b] = \{x | a \lt x \leq b
\}\)
\((a,b) = \{x | a \lt x \lt b
\}\)
- We call intervals of the form \([a,b]\) closed intervals and \((a, b)\) open intervals.
- Note: \(\infty\)
cannot define a closed interval
Sets as elements of sets
- Sets can be elements of sets
- \(\{\{1,2,3\}, a, \{b, c\}\)
- \(\{\mathbb{Q},\mathbb{R}\}\)
- The empty set can be member of a set
- A set with \(\emptyset\) as a
member is different than \(\emptyset\)!
- \(\emptyset \neq \{ \emptyset
\}\)
Set equality
Are these sets equal?
\(\{a, b, c,
d\}\) and \(\{a, b, c, b, c,
d\}\)
\(\{a, b, c,
d\}\) and \(\{a, b, \{c,
d\}\}\)
\(\{a, b, c,
d\}\) and \(\{c, d, a,
b\}\)
Set equality
Two sets are equal if (and only if) they have the same
elements.
- If they have the same elements, then they are equal,
- If they are equal, then they have the same elements.
If \(A\) and \(B\) are sets, then \(A\) and \(B\) are equal if and only if \[\forall x. (x \in A \leftrightarrow x \in
B)\] or equivalently \[\forall x. (x
\in A \to x \in B) \wedge (x \in B \to x \in A)\]
- \(\{1, 3, 5\} = \{3, 5,
1\}\)?
- \(\{1, 5, 5, 5, 3, 3, 1\}
= \{1, 3, 5\}\)?
Proving two sets are equal
Let \(A = \{1, 5, 5, 5, 3, 3, 1\}\)
and \(B = \{1, 3, 5\}\). Prove that
\(A=B\).
We want to show that \[\forall x. (x \in A
\to x \in B) \wedge (x \in B \to x \in A)\]
How many cases are there?
Set cardinality
- Finite and infinite sets
-
If there are exactly \(n\) distinct
elements in \(S\) where \(n\) is a nonnegative integer, we say \(S\) is finite. Otherwise
it is infinite.
- Cardinality
-
The cardinality of a finite set \(A\), written \(|A|\), is the number of (distinct) elements
of \(A\).
Set cardinality examples
- \(|\emptyset| =
?\)
- Let \(S\) be the
letters in the English alphabet. Then \(|S| =
?\).
- \(|\{1, 2, 3\} =
?|\)
- \(|\{\emptyset\}| =
?\)
- \(|\mathbb{Z}| =
?\)
- \(\infty\)
- Technically \(\aleph_0\), but we will explore that in a
later lecture
Subsets
- Subset
-
The set \(A\) is a
subset of \(B\) if and
only if every element of \(A\) is also
an element of \(B\).
- We write \(A \subseteq B\) to
indicate \(A\) is a subset of \(B\).
- \(A \subseteq B\) is true iff \(\forall x. (x \in A \to x \in B)\)
Proving subset relationships
- To prove \(A\) is a subset of \(B\), we show that if (any) \(x\) is a member of \(A\), then it is also a member of \(B\)
- \(\forall x. (x \in A \to x \in
B)\)
Proving subset
relationships
\[\forall x. (x \in A \to x \in
B)\]
\(\{1, 5, 5, 5, 3, 3,
1\} \subseteq \{1, 3, 5\}\)
- for each \(x\) in
\(A\), show it belongs to \(B\).
\(S \subseteq
S\) for every set \(S\)?
- Yes, since \(a \in S \to
a \in S\)
\(\emptyset \subseteq
S\) for every set \(S\)?
Yes, every element of \(\emptyset\) is in \(S\), there just aren’t any
members.
\(\forall x. x \in
\emptyset \to x \in S\) is vacuously true: \(x \in \emptyset\) is always false.
Proving subset
relationships
Let S be the set of integers with squares less than 100.
- \(S \subseteq
\mathbb{N}\) ?
Proof:
- \(-2 \in S\) since \((-2)^2 = 4 < 100\)
- \(-2 \not \in \mathbb{N}\)
\(\square\)
Set equality revisited
- Recall our definition of set equality: We write \(A = B\) if
\[ \forall x. (x \in A \leftrightarrow x
\in B)\]
- But this is equivalent to
\[ \forall x. (x \in A \to x \in B) \wedge
(x \in B \to x \in A)\]
- So another way to define set equality is in terms of subsets:
\[ A \subseteq B \wedge B \subseteq A
\]
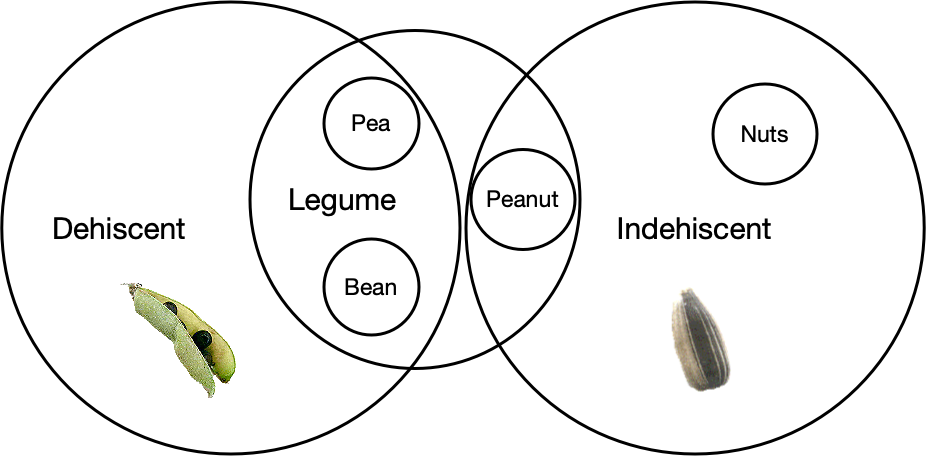
Proper subsets
- Proper subset
-
If \(A \subseteq B\) but \(A \neq B\), then \(A\) is a proper subset of \(B\) \[ A \subset
B \triangleq \forall x. x \in A \to B \wedge \exists x . x \in B \wedge
x \not \in A \]
- Peanut \(\subset\)
Legume ?
- Yes! Any \(x \in\)
Peanut is also in Legume.
- Proper since Bean \(\in\) Legume, but Bean \(\not\in\) Peanut
- Legume \(\subset\)
Indehiscent ?
- No! Bean \(\in\)
Legume, but Bean \(\not\in\)
Indehiscent
- Peanut \(\subset\)
Indehiscent ?
- Yes! Any \(x \in\)
Peanut is also in Indehiscent
- Proper since Nuts \(\in\) Indehiscent, but Nuts \(\not\in\) Indehiscent
Practice: True or False?
\(\mathbb{B} \subset
\mathbb{R}\)
\(\mathbb{Z} \subseteq
\mathbb{N}\)
\(-3 \subseteq
\mathbb{R}\)
\(\{1,2\} \not\in
\mathbb{Z}^{+}\)
\(\emptyset \subseteq
\emptyset\)
\(\emptyset \subset
\emptyset\)
\(\{x\} \subseteq
\{x\}\)
\(\{x\} \in \{x, \{x\}
\}\)
\(\{x\} \subseteq \{x,
\{x\} \}\)
\(\{x\} \in
\{x\}\)
\(\{\{x\}\} \subset
\{x, \{x\} \}\)
Power sets
- Power sets
-
The set of all subsets of a set \(A\),
written \(\mathcal{P}(A)\) is called
the power set of \(A\).
Example: If \(A = \{a,
b\}\), then \[ \mathcal{P}(A) = \{
\emptyset, \{a\}, \{b\}, \{a, b\}\} \]
What is the cardinality of \(\mathcal{P}(A)\)?
If a set has \(n\) elements, then the cardinality of its
power set is \(2^{n}\).
Sets with those little
numbers
Tuples
- The ordered n-tuple \((a_1, a_2,
..., a_n)\) is the ordered collection that has \(a_1\) as its first element, \(a_2\) as its second element, etc, until
\(a_n\), its last element.
Tuples
pair: ![]()
3-tuple: \((1, 3,
5)\)
5-tuple: \((1, 5, 5,
3)\)
Order and repetition matter with n-tuples
![]()
\((1, 5, 5, 3) \neq
(1, 3, 5)\)
Cartesian Product
- Cartesian Product
-
The cartesian product of two sets \(A\) and \(B\), written \(A
\times B\) is the set of (all) ordered pairs where \(a \in A\) and \(b
\in B\).
\[A \times B \triangleq \{ (a, b) ~|~ a
\in A \wedge b \in B \}\]
Example: Let \(A = \{a,
b\}\) and \(B = \{1, 2, 3\}\).
\[A \times B = \{(a, 1), (a, 2), (a, 3), (b,
1), (b, 2), (b, 3)\}\]
- Relation
-
A subset \(R\) of the cartesian product
of \(A\) and \(B\), \(R \subset
A \times B\) is called a relation from the set \(A\) to the set \(B\).
Cartesian Product
- Cartesian Product
-
The cartesian product of the sets \(A_1, A_2, ..., A_n\), written \(A_1 \times A_2 \times ... \times A_n\) is
the set of ordered n-tuples \((a_1, a_2, ...,
a_n)\) where \(a_i\) belongs to
\(A_i\) for \(i \in [1, n]\).
\[A_1 \times A_2 \times ... \times A_n
\triangleq \{ (a_1, a_2, ..., a_n) ~|~ a_i \in A_i \text{ for } i \in
[1, n] \}\]
Example: Let \(A = \{0,
1\}\), \(B = \{1, 2\}\), and
\(C=\{0,1,2\}\). \[\begin{align}
A \times B \times C = \{ &(0,1,0), (0,1,1), (0,1,2), \\
&(0,2,0), (0,2,1), (0,2,2), \\
&(1,1,0), (1,1,1), (1,1,2), \\
&(1,2,0), (1,2,1), (1,2,2)\}
\end{align}\]
Those little numbers
- What is \(\mathbb{R}^{2}\)?
\(\mathbb{R}^2 = \mathbb{R} \times
\mathbb{R}\)
- What about \(\mathbb{R}^{3}\)?
\(\mathbb{R}^3 = \mathbb{R} \times
\mathbb{R} \times \mathbb{R}\)
- In general, for a set \(A\), \[\begin{align}
A^{n} &= A \times A \times ... \times A \\
&= \{(x_1, x_2, ..., x_n)~|~ x_1, x_2, ..., x_n \in A\}
\end{align}\]
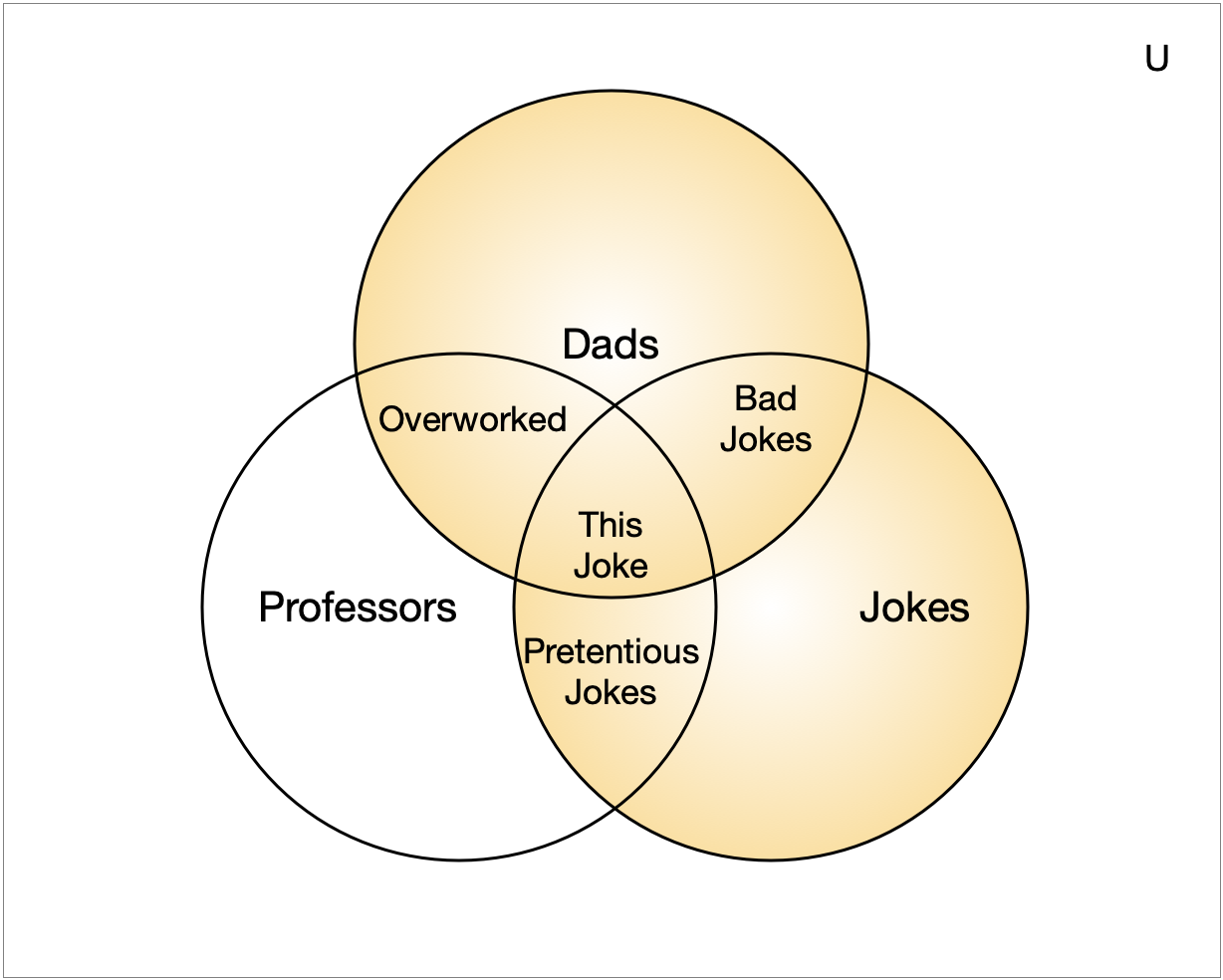
Union
- Union
-
Let \(A\) and \(B\) be sets. The union of \(A\) and \(B\), written \(A
\cup B\) is the set \[\{ x ~|~ x \in A
\vee x \in B \}\]
Example:
- What is \(\{1,2,3\} \cup
\{3, 4, 5\}\)
Dads \(\cup\) Jokes
![]()
Intersection
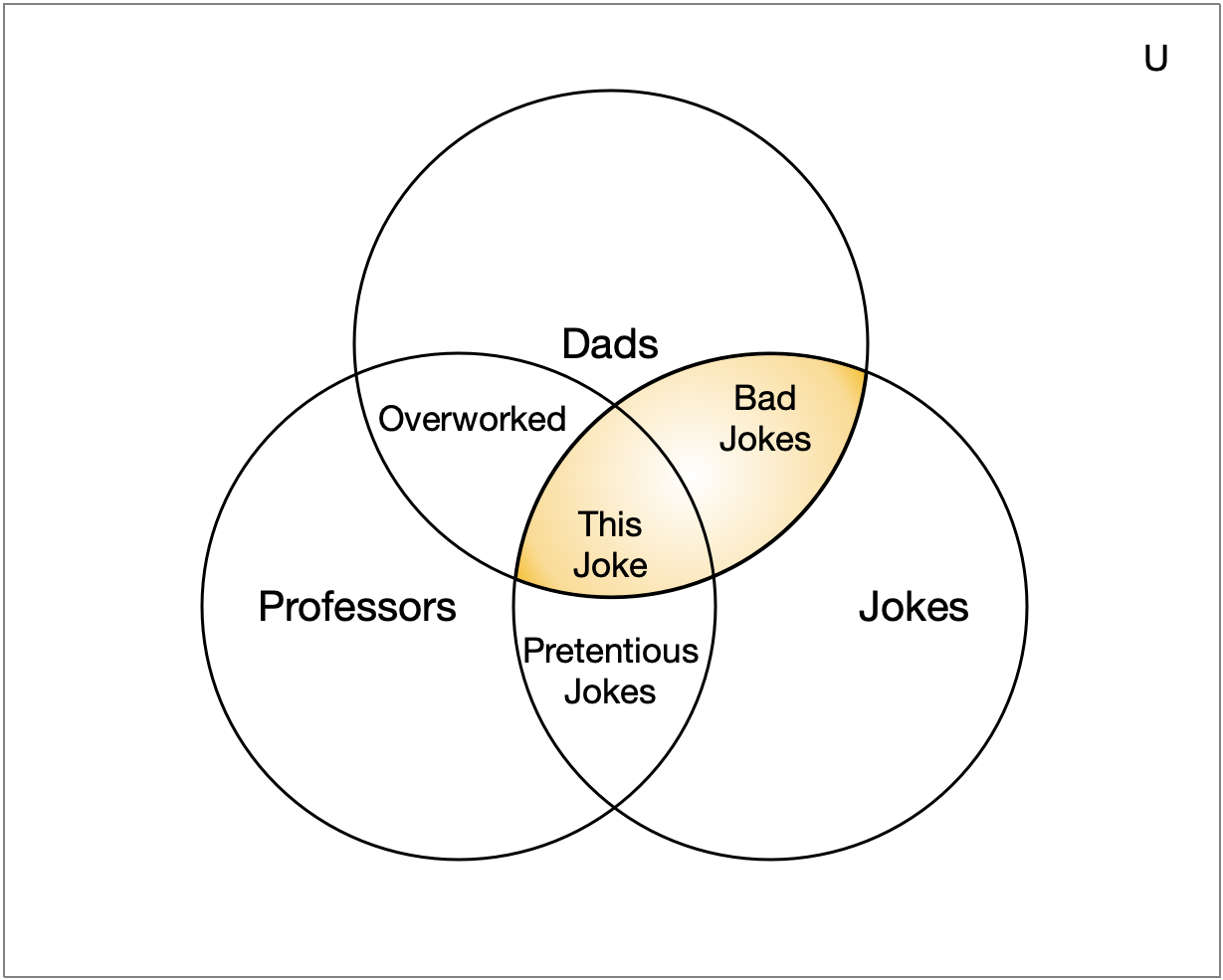
- Intersection
-
Let \(A\) and \(B\) be sets. The intersection of
\(A\) and \(B\), written \(A
\cap B\) is the set \[\{ x ~|~ x \in A
\wedge x \in B \}\]
Example:
- What is \(\{1,2,3\} \cap
\{3, 4, 5\}\)
- What is \(\{1,2,3\} \cap
\{4, 5, 6\}\)
Dads \(\cap\) Jokes
![]()
Generalized Unions and
Intersections
- Let \(A_1, A_2, ..., A_n\) be an
indexed collection of sets. We define
\[\begin{align}
\bigcup_{i=1}^{n} A_i &= A_1 \cup A_2 \cup ... \cup A_n \\
\bigcap_{i=1}^{n} A_i &= A_1 \cap A_2 \cap ... \cap A_n \\
\end{align}\]
There are well defined since union and intersection are
associative.
- What abount infinite sets?
- For \(i \in [1,2,...]\) let \(A_i = {i, i+1, i+2,...}\). Then,
\[ \bigcup_{i=1}^{n} A_i =
\{i,i+1,i+2,...\} = ???\]
\[ \bigcap_{i=1}^{n} A_i = A_1 \cap A_2
\cap ... \cap A_n\]
\[\{n,n+1,n+2,...\} = A_n\]
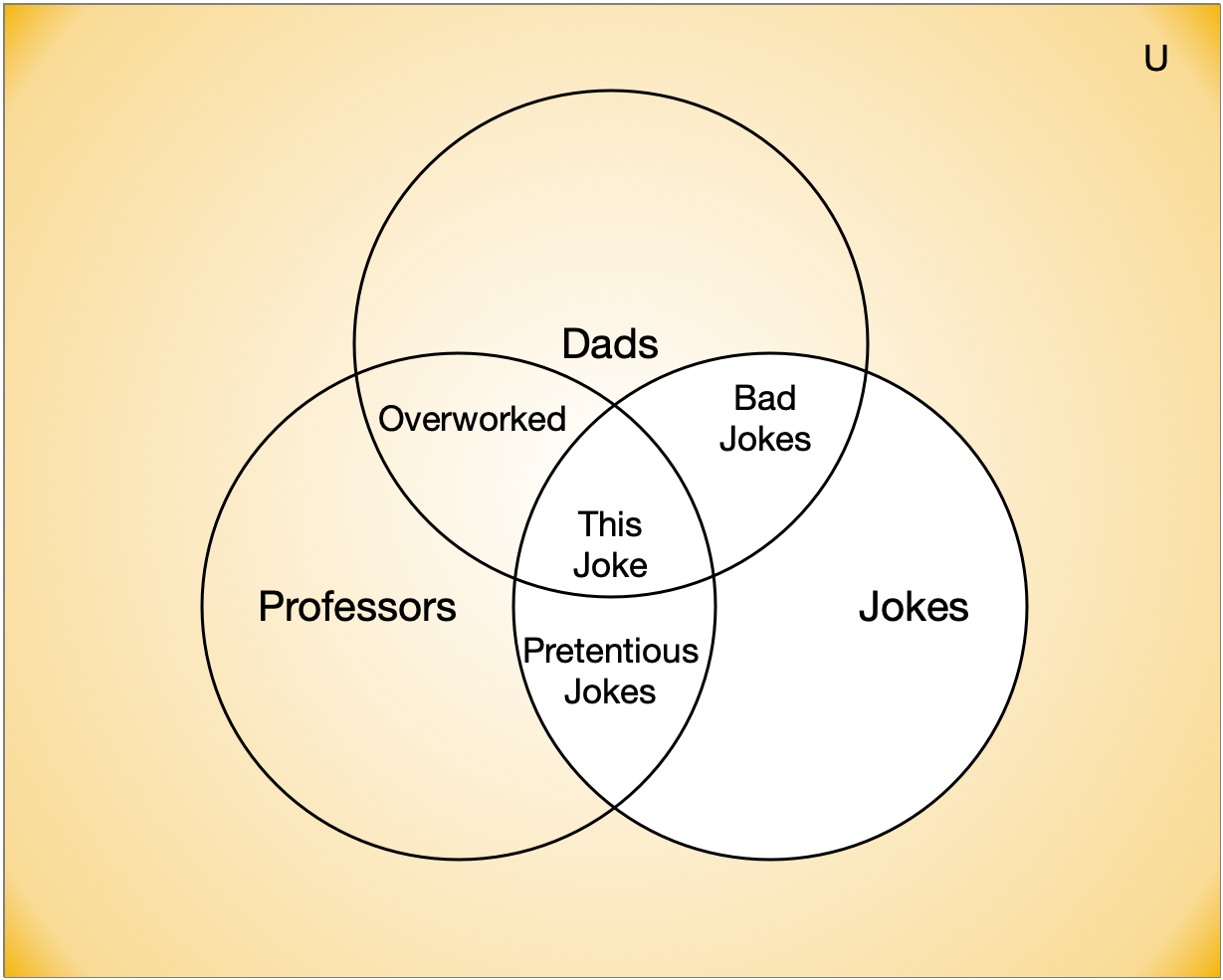
Complement
- Complement
-
Let \(A\) be a set. The
complement of \(A\) (with
respect to \(U\)), written \(\overline{A}\) is the set \(U - A\): \[\{x
\in U ~|~ x \not\in A \}\]
Example:
- If \(U\) is the
positive integers less than 100, what is the complement of \(\{x ~|~ x \gt 70 \}\)
\(\overline{\text{Jokes}}\)
![]()
Set difference
- Difference
-
Let \(A\) and \(B\) be sets. The difference of
\(A\) and \(B\), written \(A
- B\) (also sometimes written \(A \
B\)) is the set containing elements of \(A\) that are not in \(B\). Also called the complement of \(B\) with respect to \(A\). \[\{ x ~|~
x \in A \wedge x \not\in B \}\]
Example:
- What is \(\{1,2,3\} -
\{3, 4, 5\}\)
Dads \(-\) Jokes
![]()
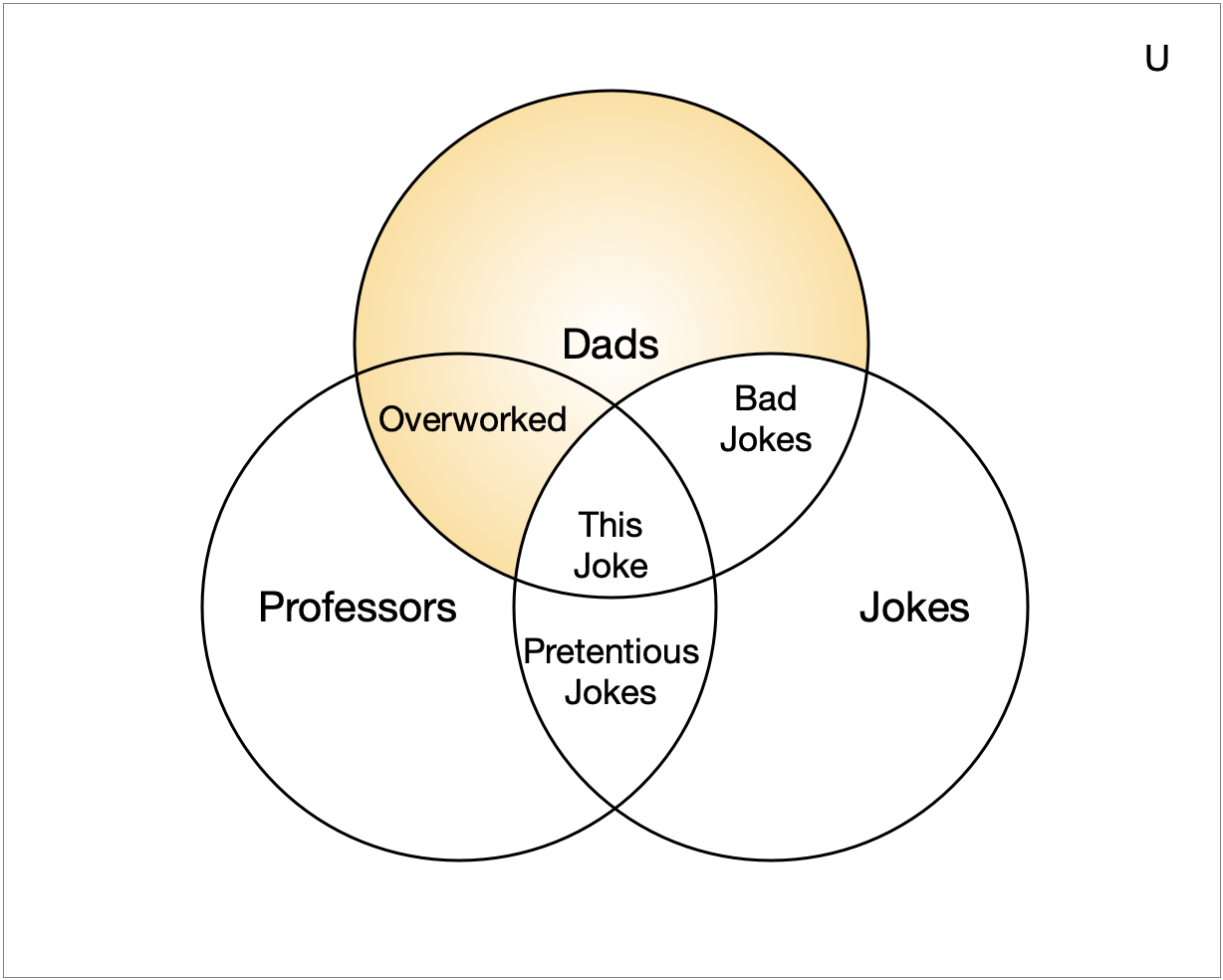
Symmetric Difference
- Symmetric difference
-
Let \(A\) and \(B\) be sets. The symmetric
difference of \(A\) and \(B\), written \(A
\oplus B\) is the set \[(A - B) \cup
(B - A)\]
Example:
\(U = \{0,1,2,3,4,5,6,7,8,9,10\}\)
\(A = \{1,2,3,4,5\}\) \(B = \{4,5,6,7,8\}\)
Dads \(\oplus\) Jokes
![]()
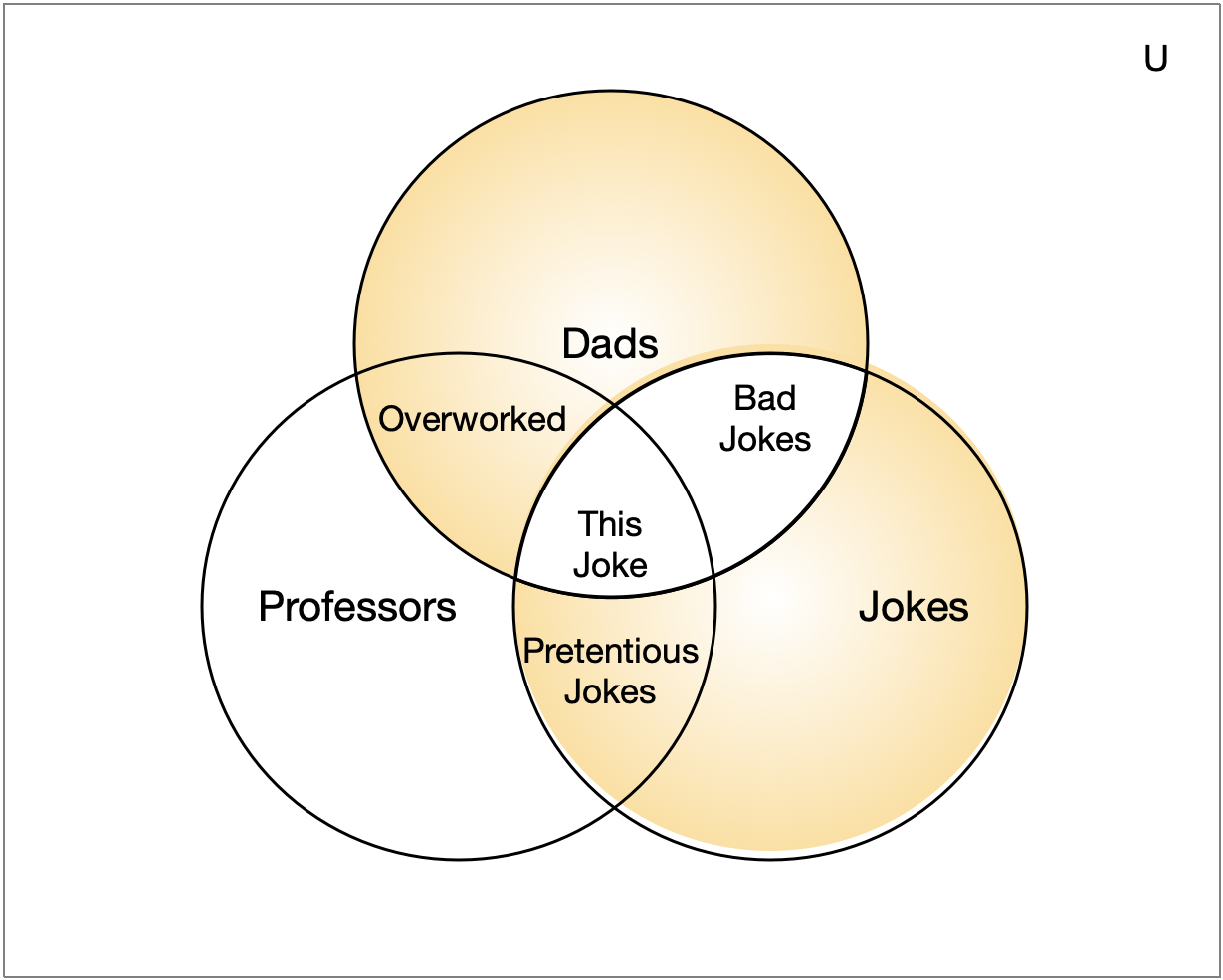
Cardinality of unions
\(U =
\{0,1,2,3,4,5,6,7,8,9,10\}\)
\(A = \{1,2,3,4,5\}\) \(B = \{4,5,6,7,8\}\)
\[|A \cup B| = |A| + |B| - |A \cap
B|\]
Set operations
| Intersection |
\(A \cap
B\) |
\(\{x: x \in A
\wedge x \in B\}\) |
| Union |
\(A \cup
B\) |
\(\{x: x \in A
\vee x \in B\}\) |
| Difference |
\(A -
B\) |
\(\{x: x \in A
\wedge x \not\in B\}\) |
| Symmetric difference |
\(A \oplus
B\) |
\(\{x: x \in
(A-B) \wedge x \in (B-A)\}\) |
| Complement |
\(\overline{A}\) |
\(\{x : x
\not\in A\}\) |
Boolean Algebra
Set theory and propositional calculus are both instances of an
algebraic system called a Boolean algebra (after George
Boole).
Set theory operators have analogous operators in propositional
calculus: \[\begin{align}
A \cap B \qquad &\sim \qquad A \wedge B \\
A \cup B \qquad &\sim \qquad A \vee B \\
\overline{A} \qquad &\sim \qquad \neg A
\end{align}\]
All sets are assumed to be subsets of the universal set \(U\).
Laws of propositional logic
Remember these?
| Idempotence |
\(p \vee p \equiv p\) |
\(p \wedge p \equiv p\) |
| Associativity |
\((p \vee q) \vee r \equiv p \vee (q \vee
r)\) |
\((p \wedge q) \wedge r \equiv p \wedge (q
\wedge r)\) |
| Commutativity |
\(p \vee q \equiv q \vee p\) |
\(p \wedge q \equiv q \wedge
p\) |
| Distributivity |
\(p \vee (q \wedge r) \equiv (p \vee q)
\wedge (p \vee r)\) |
\(p \wedge (q \vee r) \equiv (p \wedge q)
\vee (p \wedge r)\) |
| Identity |
\(p \vee \textsf{F} \equiv p\) |
\(p \wedge \textsf{T} \equiv
\textsf{T}\) |
| Domination |
\(p \wedge \textsf{F} \equiv
\textsf{F}\) |
\(p \vee \textsf{T} \equiv
\textsf{T}\) |
| Double Complement |
\(\neg \neg p \equiv p\) |
|
| Complement |
\(p \wedge \neg p \equiv
\textsf{F}\)
\(~~~~~~\neg
\textsf{T} \equiv \textsf{F}\) |
\(p \vee \neg p \equiv \textsf{T}\)
\(\neg \textsf{F} \equiv
\textsf{T}\) |
| De Morgans |
\(\neg (p \vee q) \equiv \neg p \wedge
\neg q\) |
\(\neg (p \wedge q) \equiv \neg p \vee
\neg q\) |
| Absorption |
\(p \vee (p \wedge q) \equiv
p\) |
\(p \wedge (p \vee q) \equiv
p\) |
Set identities
They work for sets too!
| Idempotence |
\(p \cup p \equiv p\) |
\(p \cap p \equiv p\) |
| Associativity |
\((p \cup q) \cup r \equiv p \cup (q \cup
r)\) |
\((p \cap q) \cap r \equiv p \cap (q \cap
r)\) |
| Commutativity |
\(p \cup q \equiv q \cup p\) |
\(p \cap q \equiv q \cap p\) |
| Distributivity |
\(p \cup (q \cap r) \equiv (p \cup q) \cap
(p \cup r)\) |
\(p \cap (q \cup r) \equiv (p \cap q) \cup
(p \cap r)\) |
| Identity |
\(p \cup \emptyset \equiv p\) |
\(p \cap \textsf{U} \equiv
\textsf{U}\) |
| Domination |
\(p \cap \emptyset \equiv
\emptyset\) |
\(p \cup \textsf{U} \equiv
\textsf{U}\) |
| Double Complement |
\(\overline{\overline{p}} \equiv
p\) |
|
| Complement |
\(p \cap \overline{p} \equiv
\emptyset\)
\(~~~~~~\overline{\textsf{U}} \equiv
\emptyset\) |
\(p \cup \overline{p} \equiv
\textsf{U}\)
\(\overline{\emptyset} \equiv
\textsf{U}\) |
| De Morgans |
\(\overline{(p \cup q)} \equiv
\overline{p} \cap \overline{q}\) |
\(\overline{(p \cap q)} \equiv
\overline{p} \cup \overline{q}\) |
| Absorption |
\(p \cup (p \cap q) \equiv p\) |
\(p \cap (p \cup q) \equiv p\) |
Proof of DeMorgan’s 2nd Law
Theorem: \(\overline{(p
\cap q)} \equiv \overline{p} \cup \overline{q}\)
Proof. We prove this in two steps:
Step 1. \(\overline{(p \cap q)} \subseteq
\overline{p} \cup \overline{q}\)
Step 2. \(\overline{p} \cup \overline{q}
\subseteq \overline{(p \cap q)}\)
Proof of DeMorgan’s 2nd Law
Step 1. \(\overline{(p \cap q)} \subseteq
\overline{p} \cup \overline{q}\)
\[\begin{align}
x \in \overline{(p \cap q)} & \qquad \text{by
assumption} \\
x \not\in (p \cap q) & \qquad \text{defn. of
complement} \\
\neg ((x \in p) \wedge (x \in q)) & \qquad \text{defn.
of intersection} \\
\neg (x \in p) \vee \neg (x \in q) & \qquad \text{De
Morgan's (prop. logic)} \\
(x \not\in p) \vee (x \not\in q) & \qquad \text{defn.
of negation} \\
(x \in \overline{p}) \vee (x \in \overline{q}) & \qquad \text{defn.
of complement} \\
(x \in \overline{p}) \cup (x \in \overline{q}) & \qquad \text{defn.
of union}
\end{align}\]
Proof of DeMorgan’s 2nd Law
Step 2. \(\overline{p} \cup \overline{q}
\subseteq \overline{(p \cap q)}\)
\[\begin{align}
x \in \overline{p} \cup \overline{q} & \qquad \text{by
assumption} \\
(x \in \overline{A}) \vee (x \in \overline{B}) & \qquad \text{defn.
of union} \\
(x \not\in A) \vee (x \not\in B) & \qquad \text{defn. of
complement} \\
\neg(x \in A) \vee \neg(x \in B) & \qquad \text{defn. of negation}
\\
\neg((x \in A) \wedge (x \in B)) & \qquad \text{De Morgan's
(prop. logic)} \\
\neg((x \in (A \cap B)) & \qquad \text{defn. of intersection} \\
x \in \overline{A \cap B} & \qquad \text{defn. of complement} \\
\end{align}\]
Partitions
- Disjoint sets
-
Two sets \(A\) and \(B\) are disjoint if their
intersection is empty: \(A \cap B =
\emptyset\)
- Partition
-
A partition of a non-empty set \(A\) is a collection of non-empty subsets of
\(A\) such
-
that each element of \(A\) is in
exactly one of the subsets.
\[\begin{align}
A &= \{1,2,3,4,5,6,7,8,9\} \\
A_1 &= \{2,4,6\} \\
A_2 &= \{1,3,5\} \\
A_3 &= \{7,8,9\}
\end{align}\]
Russell’s Paradox
Naive set theory leads to paradoxes
- Let \(S\) be the
set of all sets which are not members of themselves.
- True or False: \(S \in
S\) ?
- Paradox!
![]()
Axiomatic set theory
- Today, Zermelo-Fraenkel set theory with the axiom of choice (ZFC) is
the most common foundational theory for mathematics.
- Avoids most paradoxes by restricting what sets are
definable.
- Everything is a set
- No universal set
- No “unrestricted comprehensions” \[\exists S. \forall x. ( x \in S \leftrightarrow
\neg (x \in x))\]
- In other words, sets are no longer defined as a
collection of elements that share a common property
